Wie wir die Temperatur in den Wolken messen

Ein Regenschauer auf 24 GHz

Auf 24 GHz hängt das Himmelsrauschen sehr stark von der Luftfeuchtigkeit ab, weil die Wassermoleküle in der Lage sind, bei dieser Frequenz Radiowellen zu absorbieren, was sie dann schneller um sich rotieren läßt. Das macht die Beobachtungsbedingungen sehr stark wetterabhängig. Am Nachmittag des 19. Oktober 2019 war die 24 GHz Antenne auf irgendeine leere Himmelsgegend gerichtet belassen, während die Empfangsleistung ständig aufgezeichnet wurde. Über die nächsten 6 Stunden kann man bereits ein langsames und systematisches Ansteigen des Rauschens um etwa 0.5 dB bemerken. Aber hinzu kamen noch eine Reihe von Regenschauern zwischen UT 13:00 und UT 15:00. Während jeder Schauer aus der dazugehörigen dunklen Wolke herunterkam, erhöhte sich das Rauschen um fast 1 dB.

Dunkle Wolken zeigen sich auf 24 GHz recht deutlich, weil Wassermoleküle bei 22.2 GHz sehr gut absorbieren können und ihr hoher Wasserdampfanteil sie dadurch hell erscheinen läßt. Dies macht sich auf zweierlei Weise bemerkbar: Während die Wolke sich zwischen Sonne und Antenne schiebt, schwächt sie das Radiosignal ab. Aber richten wir die Antenne auf den 'leeren' Himmel neben der Sonne, können wir das Rauschen der Wärmestrahlung der Wolke selber messen. Eine Zeit mit ziemlich schlechtem Wetter kann man dazu benutzen, die physische Temperatur von Regenwolken zu messen. Der theoretische Hintergrund ist derselbe wie in Erdatmosphäre: Der empfangene Radiofluss (als Antennentemperatur ausgedrückt) der Sonne wird durch die Absorption einer Wolke mit der optischen Dicke τ (griech. Buchstabe 'tau') vermindert: T = T₀ * exp(-τ) wobei T₀ die Antennentemperatur der unabgeschwächten Sonne ist. Die Wolke gibt aber auch Wärmestrahlung ab, deren Stärke von ihrer Temperatur T_cloud und ihrer optischen Dicke abhängt: Ihre Antennentemperatur beträgt T = T_cloud * (1 - exp(-τ)) Diese Formel hat zwei Grenzfälle: Die Emission einer ziemlich transparenten Wolke ('optisch dünn' τ ≪ 1) nimmt mit der optischen Dicke zu T = T_cloud * (1 - exp(-τ)) ≈ T_cloud * (1 - (1-τ)) = T_cloud * τ Die gemessene Antennentemperatur hängt also vom Produkt der Wolkentemperatur und der optischen Dicke ab: Wenn wir die Wolkentemperatur wüssten oder schätzen könnten, ergibt die Messung die optische Dicke; ist andererseits die optische Tiefe bekannt, können wir die Temperatur der Wolke bestimmen. Der andere Fall ist eine undurchsichtige oder optisch dicke Wolke (τ ≫ 1): sie blockiert die Sonnenstrahlung, gibt aber ihrerseits Strahlung ab, deren Stärke nur von ihrer physischen Temperatur abhängt: T = T_cloud weil für große x gilt exp(-x) → 0. Eine Messung gibt uns also direkt die wahre Wolkentemperatur.
Dies bedeutet, dass eine transparente Wolke das Sonnensignal nur wenig abschwächt, aber auch selber nur wenig emittiert. Eine undurchsichtige Wolke wird die Sonnenstrahlung blockieren, aber selber als eine Quelle am Himmel sichtbar sein, die etwas heller als der blaue Himmel ist. Als grobe Grenze zwischen optisch dünn und dick können wir τ = 1 betrachten. Dies bedeutet eine Abschwächung des Sonnensignals um 10*log10(exp(1)) = 4.343 dB.

An einem miesen Tag ...

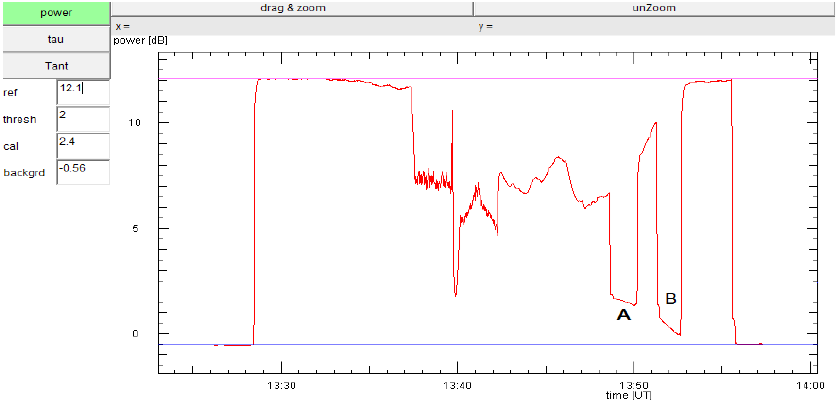
Der 27. Juli 2015 war ein Tag mit einem ständig irgendwie bedecktem Himmel, aber ich brauchte einige Positionsmessungen am 24 GHz Spiegel, und begann die Sonne nachzuführen. Die Rohdaten zeigt die Grafik: Das Sonnensignal schien zunächst stabil und hinreichend gut zu sein. Um UT 13:38 begann ich eine Messung der wahren Sonnenposition, obwohl das Signal leicht abfiel. Aber als das Signal noch viel stärker einbrach, gab ich um UT 13:42 einfach auf ... Bis dahin war das Signals um mehr als 4.3 dB unter das Normalniveau gefallen. Es war klar, dass gerade eine große und feuchte Wolke vorbeizog. Die Schwäche des Sonnensignals würde ein Maß für die optische Dicke der Wolke geben. Daher schwenkte ich die Antenne zweimal, bei A and B, um etwa 5° ostwärts von der Sonne weg, um dort die Wärmestrahlung der Wolke zu messen.
Man beachte, dass vor und nach diesem Ereignis das Sonnensignal auf dem gleichen Wert von 12.1 dB war (angedeutet durch die lila Linie). Gleichermaßen ergab das Himmelsrauschen - einige Grad östlich der Sonne - denselben Untergrundswert von -0.56 dB (blaue Linie). Daher können wir getrost davon ausgehen, dass diese beiden Parameter sich während der ganzen Zeit konstant blieben, und dass der Vorübergang der Wolke nur ein relativ kurzes einzelnes Ereignis war.

Der gemessene Radiofluss von der Sonne, die durch eine Regenwolke verdeckt ist, besteht aus drei Teilen: das abgeschwächte Sonnensignal, die Wärmestrahlung der Wolke, und das Eigenrauschen des Empfangssystems: p = g * (T_sun * exp(-τ) + T_cloud * (1 - exp(-τ)) + T_sys) mit dem Faktor g ('gain'), der die Umrechnung zwischen Temperatur und angezeigter Leistung darstellt.
Zur Auswertung betrachten wir die Ergebnisse dreier Einzelmessungen: Das Signal von 12.1 dB der unbedeckten Sonne entspricht der Leistung: p₀ = g * (T_sun + T_sky(ε) + T_sys) und die 0.56 dB des Untergrundrauschens: backgrd = g * (T_sky(ε) + T_sys) Auch haben wir mit 2.4 dB das Bodenrauschen zum Zwecke der Kalibrierung (290 K) gemessen: cal = g * (290 K + T_sys)

Während eine strikte Herleitung etwas komplizierte Formeln liefert, können wir sich (hinterher) davon überzeugen, dass wir auch genügend genaue Ergebnisse erhalten, wenn wir das schwache Rauschen des Himmels und des Untergrunds gegenüber dem starken Sonnensignal vernachlässigen: exp(-τ) ≈ (p - backgrd) / (p₀ - backgrd) ≈ p / p₀ was bedeutet, dass das Verhältnis von abgeschwächtem Sonnensignal p und unabgeschwächtem Wert p₀ in jedem Moment die optische Dicke misst. Mit den dB Werten ergibt dies einfach die Differenz τ = (p_{0 dB} - p_dB) /4.343
Im Plot haben wir dann geeignete blaue Punkte markiert, so dass der sich daraus ergebende Streckenzug den zeitlichen Verlauf der optichen Dicke interpoliert, insbesondere während der Intervalle A and B, als das Himmelsrauschen neben der Sonne gemessen wurde.

Der letzte Schritt der Interpretation ist die Berechnung der Temperatur in der Wolke. Dem gemessenen Himmelsrauschen entspricht: p_cloud = g * (T_cloud * (1 - exp(-τ)) + T_sys) woraus wir mit Näherungen wie oben bekommen T_cloud ≈ 290 K * (p_cloud - backgrd)/(cal - backgrd) / (1- exp(-τ)) Der Plot zeigt, dass die Temperatur bei A und B jeweils ziemlich konstant ist und nahe bei 300 K liegt - wie man es auch vernünftigerweise hätte vermuten können.
Siehe DUBUS 1/2016, 70.