Wie wir die Eigenschaften der Erdatmosphäre messen

Die Atmosphäre unserer Erde beeinflusst die Stärke von Radiosignalen einer Himmelsquelle in zweifacher Weise: sie schwächt nicht nur das Signal ab, sondern weil die Luft selbst auch eine Temperatur hat, gibt sie auch Wärmestrahlung ab, die auf alle Beobachtungen einen Vordergrundsschleier aus Rauschen legt. Das Himmelsrauschen kommt zum Eigenrauschen des Empfangssystems hinzu und begrenzt dadurch die Empfindlichkeit der Anlage. Auf Frequenzen oberhalb von etwa 10 GHz wird dies immer wichtiger und kann nicht länger vernachlässigt werden. Beide Wirkungen müssen berücksichtigt werden, wenn wir radioastronomische Messungen oder die gemessenen Signalstärken von Satelliten und Raumsonden auswerten möchten. Beide Einflüsse sind frequenzabhängig und werden mit höherer Frequenz stärker, um schliesslich das Radiofenster der Atmosphäre zu schliessen. Weil sie mit der Nähe zum Horizont anwachsen, ist es möglich, das Himmelsrauschen von Systemrauschen zu trennen, welches unabhängig von der Elevation ist. Da nun die Variation mit dem Elevationswinkel einem einfachen Gesetz folgt, braucht es nur zwei Parameter, den Zustand der Atmosphäre zu beschreiben, der vom Wetter abhängig ist, und vor allem der Luftfeuchtigkeit: dies ist die Absorption in Richtung Zenit, und die Antennentemperatur des Himmelsrauschens am Zenit. Da die mittlere (physische) Temperatur der Luft nahe bei der Bodentemperatur liegt, ist bereits einer der beiden Parameter ausreichend. Wenn wir z.B. die Zenittemperatur kennen, können wir die wahre Systemtemperatur bestimmen, und jegliche Messungen in Antennentemperaturen ausdrücken.

Grundsätzliches über Strahlung in der Atmosphäre

Da die Atmosphäre eine lediglich dünne Schicht um den Erdball (Radius 6400 km) bildet, können wir sie uns als eine planparalle Schicht mit der Dicke H (etwa 8 km: die Troposphäre) und einer etwa konstanten Temperatur (etwa 290 K) denken.
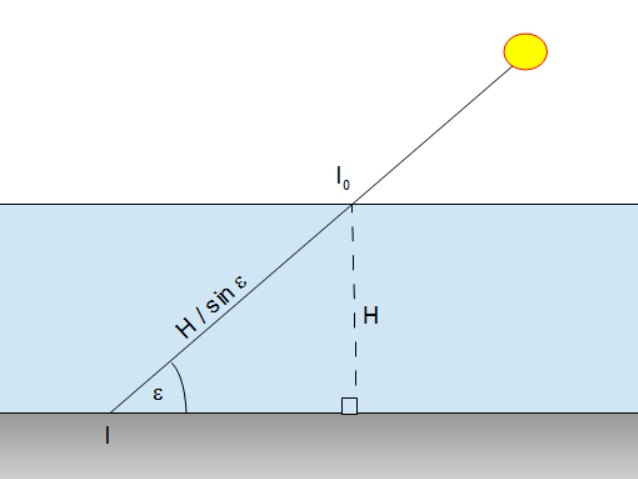
Wenn eine Radioquelle, wie die Sonne, auf einem Elevationswinkel ε beobachtet wird, müssen die Radiowellen durch eine Luftsäule der Länge L = H/sin ε laufen, die größer ist als die Säule H in Richtung Zenit. Die Leistung des Sonnensignals wird um einen Betrag abgeschwächt, der mit der Länge der Säule zunimmt, und beträgt daher p(ε) = p₀ * exp(-κ*L) = p₀ * exp(-κ*H/sin ε) = p₀ * exp(-τ/sin ε) Hier ist p₀ die Leistung der auf die Atmosphäre einfallende Strahlung. Der Absorptionskoeffizient κ (griechischer Buchstabe "kappa") gibt an, um welchen Anteil die Strahlungsleistung beim Durchgang durch eine Luftschicht der Länge 1 m abgeschwächt wird. Die Größe 1/κ hat also die Dimension einer Länge; sie kann als diejenige Wegstrecke gedacht werden, auf der die Strahlung in die Schicht eindringen kann. Dies ist sehr ähnlich der Sichtbarkeit in der Meteorologie, die die Durchsichtigkeit von Nebel beschreibt, indem man die Entfernung angibt, bis zu der Gegenstände noch klar gesehen werden können. Der Anteil, durch den das Signal abgeschwächt wird, hängt vom Produkt τ = κ*H ab, aber nicht von κ oder H einzeln, weil ein dünnes aber stark absorbierendes Material das Signal genauso stark abschwächt wie eine dicke Schicht aus transparenterer Substanz. Deshalb ist es nützlich, die Größe τ (griechisch "tau") als die optische Dicke der Atmosphäre in Richtung Zenit zu definieren.
Um aus der gemessenen Leistung der Sonne die Abschwächung zu bestimmen, benötigten wir die Leistung der einfallenden Strahlung. Da wir diese aber nicht kennen oder messen können, ist es praktischer, als eine Vergleichgröße die bei einer Referenzelevation gemessene Leistung zu nehmen, z.B. am Zenit: p(ε)/p(90°) = exp(-τ/sin ε) / exp(-τ) = exp(-τ*(1-1/sin ε)) Es ist ausserdem nützlich, die Luftmasse 'Airmass' AM = 1/sin ε einzuführen, die beschreibt, wie die Luftsäule mit fallender Elevation anwächst. Am Zenit ist AM=1. So können wir einfach schreiben p(ε)/p(90°) = exp(-τ*(1-AM))

Die Erdatmosphäre produziert auch Rauschen ...

Die Luft gibt auch selber Wärmestrahlung ab. Wenn wir - der Einfachheit halber - annehmen, dass die Lufttemperatur T_air in allen Höhen dieselbe ist wie am Erdboden, können wir die Intensität dieser Emission ausrechnen: I_EM(ε) = T_air * (1 - exp(-κ*L)) = T_air * (1 - exp(-τ*AM)) Dies bedeutet, dass in einer transparenten oder wenig absorbierenden Atmosphäre - wie es normalerweise bei Frequenzen unterhalb von etwa 30 GHz zutrifft - wir einfach schreiben können (1 - exp(-x)) ≈ x, da x ≪ 1. Daher ist die Wärmestrahlung zwar schwach, aber sie wird mit der Länge der durchlaufenen Luftsäule stärker. Ist die Atmosphäre aber völlig undurchsichtig, so ist die Intensität nur durch die Lufttemperature bestimmt. Dies ist auch der Fall bei einem Festkörper, wie der Erdboden, oder die dichten Gasschichten der Sonne. Deshalb strahlt der Erdboden im Radiobereich eine Wärmestrahlung ab, die einer Temperatur von etwa 290 K entspricht, und mit Hilfe dieser Vergleichsmessung können wir die Temperatur der Oberflächen von Sonne und Mond bestimmen.
Wir können über unsere Atmosphäre etwas erfahren, indem wir das Radiorauschen des 'leeren' Himmels (also genügend weit von Sonne, Mond, Gebäuden oder Bäumen) bei einer Anzahl von Elevationswinkeln messen, wie die Rohdaten eines derartigen 'Himmelsprofils' oder 'sky-dip' auf 1.3 GHz zeigen.

Die transparente Atmosphäre

Schauen wir uns erst eine transparente Atmophäre an, bei der die Absorption vernachlässigt werden kann. Dies bezieht sich auf Frequenzen unterhalb von etwa 10 GHz. Wenn die Antenne auf einen Elevationswinkel ε gestellt ist, besteht das gemessene Rauschen aus drei Anteilen:

das Eigenrauschen der Empfangsanlage, das durch die Systemtemperatur T_sys beschrieben wird, ist unabhängig von der Elevation
die Strahlung des Kosmischen Hintergrunds (CMB = cosmic microwave background, T_CMB = 2.7 K), die überall am Himmel gleich stark ist
die Wärmestrahlung der durchsichtigen Atmosphäre (weil die Intensität oder Strahlungsleistung proportional der Temperatur ist, messen wir sie in Temperatur): T_sky(ε) = T_air * (1 - exp(-κ*H/sinε)) ≈ T_air *τ/sinε = (T_air*τ) * AM = T_zen* AM wobei es nützlich ist, die Luftmasse AM (airmass) einzuführen und die Zenittemperatur T_zen = T_air * τ zu definieren.
bei Elevationen über etwa 70° gelangt Bodenrauschen am Rand des Parabolspiegels vorbei in die Speiseantenne ('Überstrahlen' oder 'spill-over' genannt). Da die Interpretation dieses Anteil für unsere Auswertung von keinem Nutzen ist, brauchen wir die Daten dieser hohen Elevationen nicht benutzen.

Die von der Antenne gemessene Leistung ist proportional der Summe der drei Beiträge, p(ε) = g * (T_sys + T_CMB + T_sky(ε)) wobei der Faktor g (for gain) durch eine Messung des Bodenrauschens bestimmt wird, das als eine Quelle mit bekannter Temperatur (T_ground ≈ 290 K) betrachtet werden kann: p_ground = g * (T_sys + T_ground) Da die Systemtemperatur und der Mikrowellenhintergrund nicht vom Elevationswinkel abhängen, das Himmelsrauschen aber mit der Luftmasse ansteigt, ergibt ein Plot der (linearen) Empfangsleistung als Funktion der Luftmasse AM eine gerade Linie. Somit gestaltet sich die Auswertung ganz einfach und direkt: An die Datenpunkte wird eine Gerade angepasst, die durch ihre Steigung m und den Y-Achsenabschnitt b eindeutig bestimmt ist: p(A) = b + m * AM

Die Messungen des Himmelsprofils können einfach in die verschiedenen Rauschanteile aufgespalten werden:
-- die Leistung bei AM = 1 entspricht der Antennentemperatur in Richtung Zenit: p(AM=1) = b + m = g * (T_sys + T_CMB + T_zen)
-- der Y-Achsenabschnitt b ist die Leistung, die man messen würde, wenn keine Atmosphäre vorhanden wäre. Dies ist also das Eigenrauschen der Empfangsanlage (gemessen durch die Systemtemperatur T_sys) plus der Kosmischen Hintergrundsstrahlung (T_CMB = 2.7 K): p(AM=0) = b = g * (T_sys + T_CMB)
Aus diesen Beziehungen erhalten wir die Systemtemperatur T_sys = (b * T_ground - p_ground*T_CMB) / (b - p_ground) und die Zenittemperatur, d.h. die Antennentemperatur der Atmosphäre im Zenit: T_zen = (b + m)*(T_sys + T_ground )/p_ground - T_sys - T_CMB

Auswertung des oben gezeigten Himmelsprofils auf 1.3 GHz. Wir berücksichtigen nicht die Daten mit Elevation über 70° (wegen Überstrahlen), sowie die Messung bei 15°, bei der Verdacht auf Bodenrauschen (durch Bäume) besteht.

Die absorbierende Atmosphäre

Auf Frequenzen oberhalb von etwa 10 GHz können wir die Abschwächung durch die Absorption in der Atmosphäre nicht mehr vernachlässigen. Als Beispiel liegen die Messdaten (rote Punkte) eines Himmelsprofils auf 24 GHz nicht mehr auf einer geraden Linie, sondern auf einer gekrümmten Kurve.
Aber wenn wir einen Wert für die Abschwächung in Richtung Zenit tau = AdB/4.343 schätzen und jeden Wert AM der Luftmasse durch (1 - exp(-tau*AM)) oder (1 - 10^-AdB/10*AM) ersetzen, werden die Datenpunkte im Plot derart verschoben (violette Kreise), dass sie wieder auf einer Geraden zu liegen kommen. Der Wert, der einen besten Fit mit einer Geraden erbringt, ist die gesuchte Zenitabschwächung. Zenitemperatur (in K) und -abschwächung (AdB in dB) drücken ein und dasselbe aus, nur auf verschiedene Weise; sie sind durch T_zen = T_rad * (1 - 10^-AdB/10) miteinander verbunden, wobei die Strahlungstemperatur der Atmosphäre T_rad = T_air eingeht, die nahe bei 290 K liegt. Die ITU empfiehlt als guten Schätzwert 275 K.

Da die ganze Analyse etwas mühselig ist, habe ich allen Rechungen in ein JavaScript Werkzeug getan SkyProfileAnalysis, das die eingegebenen Daten eines Himmelsprofils auswertet und daraus System- und Zenittemperatur sowie Zenitabschwächung ermittelt, wie unten gezeigt ... Siehe DUBUS 4/2023, 7

Einige Worte zu Hintergrund der Analyse: Die Stärke der Wärmestrahlung der Erdatmosphäre ist direkt verbunden mit ihrer Abschwächung, weil das Emissionsvermögen eines Körpers der Temperatur T gleich ist dem Absorptionsvermögen multipliziert mit dem Schwarzkörperspektrum (Planck-Funktion) bei dieser Temperatur. Anders ausgedrückt, strahlt ein Körper umso heller, je besser er absorbieren kann. Bei Freuqenzen unterhalb von etwa 10 GHz ist das Absorptionsvermögen unserer Atmosphäre weniger als 0.03 dB/km, was ein Signal eines Himmelskörpers um weniger als 0.2 dB, oder 5% abschwächen würde. Gewöhnlich ist ein solcher Fehler bei der Messung der Sonnen- oder Mondtemperatur nicht besorgniserregend. Daher können wir die atmosphärische Abschwächung bei diesen Frequenzen vernächlässigen. Aber da sich die Stärke des Himmelsrauschen merklich mit der Elevation verändert (wie oben gezeigt), können wir die Wärmestrahlung nicht übersehen. Bei höheren Frequenzen müssen wir allerdings sowohl Abschwächung als auch Emission der Atmosphäre ernster nehmen.

Die atmosphärische Abschwächung variiert stark mit der Frequenz

Bei Frequenzen oberhalb von etwa 10 GHz wird die Abschwächung durch die Erdatmosphäre zunehmend wichtig. Die Grafik zeigt die Zenitabschwächung bei Normalbedingungen (15° C, Luftfeuchtigkeit 58%). Die rote Kurve ist der Beitrag von Stickstoff und Sauerstoff. Die starke Absorption bei 60 GHz wird durch Sauerstoffmoleküle verursacht, die durch Aufnahme dieser Strahlung schneller rotieren können. Die blaue Kurve ist der Beitrag von Wasserdampf, der besonders bei 24 GHz absorbiert, und dessen Stärke von der Luftfeuchtigkeit und damit vom Wetter abhängt. Die schwarze Kurve ist die Summe. Vertikale rote Geraden markieren die Amateurfunkbänder. Die Abschwächung durch die Luft steigt mit der Frequenz an, und wird oberhalb 100 GHz sehr stark.

Bei ganz hohen Frequenzen ist der Himmel genauso hell wie der Erdboden

Diese Grafik zeigt die Temperatur T_zen die in Richtung Zenit gemessen würde. Im Absorptionsmaximum von Sauerstoff bei 60 GHz ist die Luft so undurchsichtig, dass der Himmel bei jedem Elevationswinkel so hell wie der Erdboden erscheint. Ebenso ist es bei allen Frequenzen über 300 GHz.