Zwei Arten, die atmosphärische Abschwächung zu messen

Die atmosphärische Abschwächung ändert sich stark mit der Frequenz

Auf ihrem Weg von einer Himmelsquelle oder Raumsonde müssen die Radiowellen durch die Erdatmosphäre laufen. Dabei passieren zwei Dinge: das Signal wird nicht nur abgeschwächt, sondern die warme Atmosphäre fügt noch ihre Wärmestrahlung dem hinzu, was wir messen. Da beide Effekte eng miteinander verknüpft sind, bedeutet es, dass je größer die Abschwächung ist, desto größer ist auch das zusätzliche Rauschen. Der Plot zeigt die Abschwächung in Richtung Zenit unter Normalbedingungen (15°C, Luftfeuchtigkeit 58%). Die rote Kurve ist der von Stickstoff und Sauerstoff verursachte Anteil. Das starke Maximum bei etwa 60 GHz wird von Sauerstoffmolekülen erzeugt, die der Strahlung Energie entziehen und dadurch schneller rotieren können. Die blaue Kurve ist der Anteil von Wasserdampf, der ein Maximum bei 22 GHz besitzt, dessen Höhe von der Luftfeuchtigkeit und damit vom Wetter abhängt. Die Summe ist durch die schwarze Kurve angedeutet. Die Absorption durch die Luftmoleküle wächst mit steigender Frequenz an, und wird für Radioverbindungen über 100 GHz ein Problem, weil die Luft ziemlich undurchsichtig wird.

Die Abschwächung hängt ab von Druck, Temperatur und Feuchtigkeit der Luft entlang des Wegs durch die Atmosphäre, deren Werte wir nur anhand ihrer Werte am Erdboden schätzen können, und darüber hinaus noch von den Wolken am Himmel (deren Wassergehalt die wirksame Luftfeuchte erhöht). Daher ist es nicht leicht, die tatsächlichen Werte über unserer Station in zuverlässiger Weise vorherzusagen. Es bestehen zwei Möglichkeiten, die tatsächliche Abschwächung entlang des Sehstrahls zu messen: Zum einen können wir die Tatsache nutzen, dass die Wärmestrahlung der Luft eng mit der Abschwächung verknüpft ist. Dies ist in Die Erdatmosphäre beschrieben. Daneben gibt es auch die direkte Messung, wie stark ein Signal (z.B. von der Sonne) abgeschwächt wird. Natürlich können wir die Leistung des Signals, bevor es in die Atmosphäre eintritt, nicht messen, aber durch den Vergleich der Empfangsleistung der Quelle bei verschiedenen Elevationswinkeln können wir sie erschließen.

Atmosphärische Abschwächung ändert sich mit der Elevation

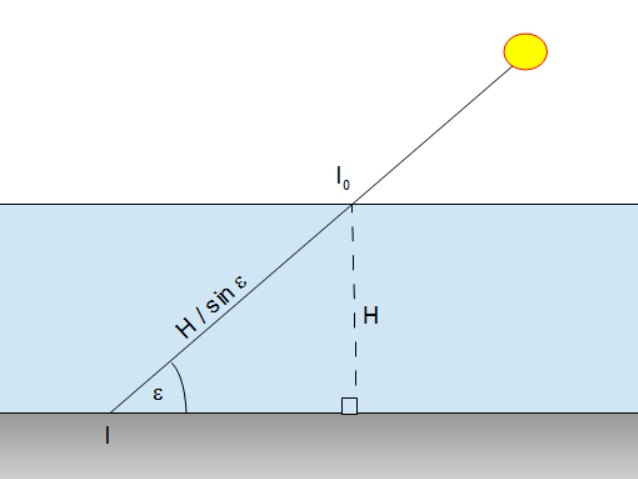
Die Abschwächung des Signals hängt vom Elevationswinkel ab, bei der die Radioquelle gesehen wird: Bei niedriger Elevation müssen die Radiowellen eine längere Luftsäule durchlaufen als bei einem hohen Elevationswinkel. Glücklicherweise ist die Erdatmosphäre eine verhältnismäßig dünne Schicht (von etwa 8 km Dicke) um den Erdball (Radius 6400 km), so dass die Länge der Luftsäule mit einer einfachen Formel: L = H/sin ε für jede Elevation ε berechnet werden kann, solange wir mehr als vielleicht 1° über dem Horizont bleiben. H ist die Höhe in Richtung Zenit. Dann beträgt die von der Sonne empfangene Leistung p(ε) = p₀ * exp(-κ*L) = p₀ * exp(-κ*H/sin ε) = p₀ * exp(-τ/sin ε) Hier bezeichnet p₀ die Leistung der Strahlung, die am oberen Rand auf die Atmosphäre eintrifft. Der Absorptionskoeffizient κ (griech. Buchstabe "kappa") gibt an, um welchen Anteil die Leistung vermindert wird, wenn das Signal durch eine Luftsäule einer Längeneinheit hindurchgeht. Die Größe 1/κ hat die Maßeinheit einer Länge; sie kann als diejenige Weglänge gedacht werden, bis zu der die Strahlung in die Schicht eindringen kann. Um wieviel das Signal geschwächt wird, hängt vom Produkt τ = κ*H ab, nicht von κ oder H getrennt: eine dünne Schicht eines stark undurchsichtigen Materials schwächt das Signal genauso stark ab wie eine dicke Schicht einer durchsichtigeren Substanz. Daher ist es sinnvoll, die Größe τ (griech. "tau"), die optische Dicke der Atmosphäre in Richtung Zenit zu definieren.
Um zwei Messungen der Sonne bei zwei recht unterschiedlichen Elevationen zu bekommen, müssten wir eine längere Zeit warten, bis die Sonne so weit wandert. Daher ist es das beste, die Sonne beispielsweise während des gesamten Nachmittags bis zum Sonnenuntergang nachzuführen, die Leistung aufzuzeichnen, und dabei in regelmäßigen Abständen auch den leeren Himmels zu messen, um in der Lage zu sein, dass Himmelsrauschen vom Sonnensignal abziehen zu können.

Wie wir es messen

Dies ist die vollständige Messung eines Nachmittags bei 8 GHz, bis zum Sonnenuntergang. Die rote Kurve ist die aufgezeichnete Leistung der Sonne, mit den Exkursionen nach unten für das Himmelsrauschen. Die kleineren Exkursionen sind Messungen der wahren Position der Sonne (für andere Zwecke). Anstatt Einzelmessungen auszuwerten, haben wir die Daten mit einem Modell verglichen:
Die blaue Kurve ist die bei jeder Elevation ε berechnete Leistung des Sonnensignals: p_sun(ε) = g * (T_source * exp(-τ sin ε) + T_air *(1-exp(-τ sin ε)) + T_sys) Die grüne Kurve ist die berechnete Leistung des Rauschens des leeren Himmels: p_sky(ε) = g * (T_air *(1-exp(-τ sin ε)) + T_CMB + T_sys) Der Factor g für 'gain' wird anhand einer zusätzlichen Messung des Bodenrauschen (hier als 'calib [dB]' bezeichnet) berechnet: p_ground = g * (T_sys + T_ground) Wir spielen nun mit den Parameterwerten in den grünen Feldern solange herum, bis sich die blauen und grünen Kurven am besten auf die Daten legen. (T_source ist die Antennentemperatur der Sonne, und T_zen = T_air * τ = 4 K die Antennentemperatur des Himmelsrauschens in Richtung Zenit).
Hieraus ergibt sich die atmosphärische Abschwächung am Zenit von 0.06 dB, was typisch für einen hellen Sommertag bei dieser recht niedrigen Frequenz ist.

Stärkere Abschwächung auf 24 GHz

Noch ein Nachmittag, der mit Nachführen und Messen der Sonne, aber auf 24 GHz, verbracht wurde. Es zeigt sich eine viel stärkere Änderung des Signals mit der Elevation: die Zenitabschwächung von 0.31 dB ist stärker, weil wir dem Absorptionsmaximum des Wasserdampfs nahe sind. Entsprechend ist die Zenittemperatur höher: 20 K.
Siehe DUBUS 1/2016, 70.

Noch stärkere Abschwächung auf 47 GHz

Hier ist ein Plot der Rohdaten eines gesamten Sommertages mit durchlaufender Nachführung und Messung der Sonne auf 47 GHz. Die kurzen Einbrüche nach unten sind Vergleichsmessungen des leeren Himmels auf jeweils gleicher Elevation, und die weniger tiefen Exkursionen sind Positionsmessungen der Sonne. Bei geringen Leistungen sind 6 Himmelsprofile und Flusskalibrierungen zu erkennen. Bei etwa UT 16:00 und UT 18:00 ist das Sonnensignal zeitweise abgeschwächt, weil die Sonne hinter zwei Kurzwellenantennen läuft.

Von den 47 GHz Daten extrahieren wir Einzelmessungen der Sonne (rote Punkte) und leerem Himmel (blau). Die Kurven stammen von einem Modell (siehe unten), welches die Nachmittagsdaten (ausgefüllte Punkte) gut erklärt. Die Daten des Vormittags (kleine Kreise) passen nicht gut zum Modell. Dies bedeutet, dass ein Modell mit demselben Wert für die Zenitabschwächung nicht ausreicht, die Daten von Vor- und Nachmittag zu erklären. Daher wurden nur die Nachmittagsdaten zur Festlegung des Modells verwendet.

Die Interpretation der Einzelmessungen auf 47 GHz (rote Punkte). Wir plotten die gemessenen Leistungen der Nachmittagsdaten in Abhängigkeit von der Luftmasse AM, und vergleichen sie mit der roten Kurve des Modells, das eine beste Anpassung an die Daten liefert. Dies ergibt eine Zenitabschwächung von 0.9 dB. Die am Zenit (Luftmasse = 1) erwartete Leistung der Sonne wäre 10 dB über dem Himmelsrauschen, und das Signal außerhalb der Erdatmosphäre (Luftmasse = 0) wäre 11.5 dB. Die zwei blauen Kurven zeigen, wie sich ein Fehler von of ± 0.1 dB in der Zenitabschwächung auswirkte, und dass die Messfehler in den Daten bei kleinen Elevationen sogar nocht besser sind.
Siehe DUBUS 2/2025, 22.