Wie wir die Halbwertsbreite der Antennenkeule (HPBW) messen
Die Halbwertsbreite (HPBW für Half-Power Beam Width) ist die Breite der Hauptkeule des Strahlungsdiagramms
einer Antenne, die auf der Hälfte des Maximalwerts gemessen wird. Die Messung der HPBW ist wichtig, weil uns
der Wert aussagt, wie gut die Antenne durch die Speiseantenne ausgeleuchtet wird, wie hoch daher der Wirkungsgrad
der Antenne ist, und wie gut das Auflösungsvermögen ist, d.h. welchen Winkeldurchmesser eine Strahlungsquelle
mindestens haben muss, um noch als Einzelobjekt erkannt zu werden. Im Idealfall wird die HPBW durch die von einer
Punktquelle (deren Winkelausdehnung kleiner als die HPBW ist) empfangene Leistung gemessen, die vor der
Antenne bewegt wird.
| Das theoretische Strahlungsdiagramm eines
kreisförmigen Antennenspiegels von Durchmesser D, der gleichmäßig beleuchtet wird, beschreibt, welche Leistung
im Sendebetrieb in die Richtung abgestrahlt oder beim Empfang aus der Richtung kommt, die den Winkel phi;
gegenüber der optischen Achse einnimmt:
p(φ) = [2λ/(πD) * J1((π D /λ) sin(φ)) / sin(φ) ]²
mit der Wellenänge λ und der Besselfunktion erster Ordnung J1(x).
Die Hauptkeule hat die Halbwertsbreite
HPBW = 59°/(D/λ)
- wobei D and λ in denselben Einheiten gegeben sind, z.B. in Meter.
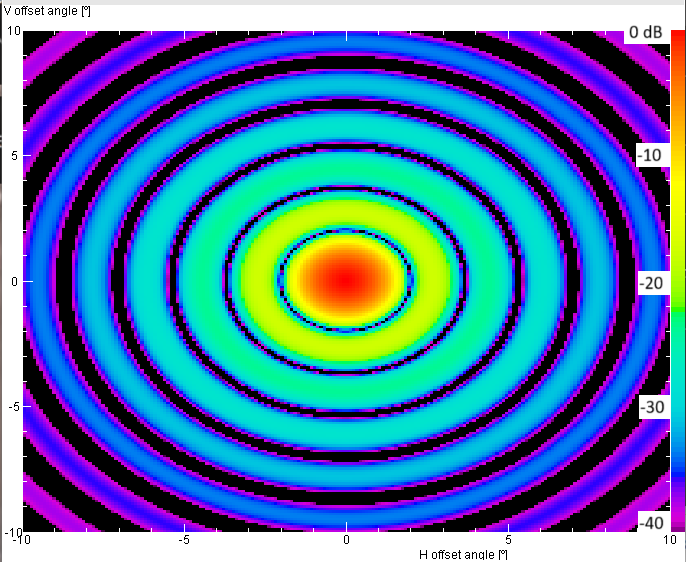
Falschfarbenkarte des theoretischen Strahlungsdiagramms einer gleichmässig ausgeleuchteten kreisförmigen Spiegels
von 8 m Durchmesser bei 1.3 GHz.
|
|
Wenn wir die HPBW messen, vergleichen wir sie mit dem theoretischen Wert, als wenn der ganze Spiegel
gleichmässig ausgeleuchtet wird. Wir berechnen den effektiven Durchmesser
Deff = (59°/HPBW) λ
der der Durchmesser eines gleichmässig beleuchteten Spiegels ist, deren Keule dieselbe Halbwertsbreite besitzt.
Dies gibt uns auch die wirksame Antennenfläche Aeff = Deff² π/4
die die Fläche ist, über die die Antenne ausgeleuchtet ist, bzw. mit der sie die Radiowellen auffängt.
Das Verhältnis von wirksamer und wahrer Fläche - oder das Quadrat des Verhältnisses von effektivem
und wahrem Spiegeldurchmesser gibt uns den (Apertur-)Wirkungsgrad:
η = (Deff/D)².
Der andere wichtige Antennenparameter ist der (lineare) Gewinn ('gain'):
G = 4 π Aeff / λ²
oder auch durch die HPBW ausgedrückt:
G = (π 59°/HPBW)²
und der Gewinn in dB relativ zum isotropen Strahler:
GdBi = 10 * log10(G)
In der Praxis ist es am besten, wenn wir die Sonne auf ihrer Wanderung über den Himmel benutzen,
weil sie auf allen Frequenzen die stärkste Radioquelle am Himmel ist, und sie sich am Himmel
aufgrund der vollkommen gleichmässigen Rotation der Erde in einer genauestens vorhersagbarer Weise
bewegt. Wir führen also einen Driftscan durch, indem wir die Antenne auf eine
Position stellen, an der die Sonne etwas später sein wird, und messen dann ununterbrochen die
Leistung während die Sonne durch die Antennenkeule zieht.
Allerdings gibt es ein kleines Problem: Die Sonne mit ihrem Winkeldurchmesser von etwa 0.5°
ist keine echte Punktquelle. Daher wird unser Messverfahren von der Halbwertsbreite der Antenne abhängen:
(a) Für Antennenkeulen, die deutlich breiter als 0.5° sind können wir die Sonne als eine hinreichend
kleine helle Quelle betrachten. Somit wird die gemessene Kurve des Driftscans direkt die Abhängigkeit
der Antennenempfindlichkeit vom Winkelabstand der Sonne von der Keulenmitte zeigen.
(b) Ist die Antennenkeule schmaler als der Sonnendurchmesser, zeigt die Driftscankurve wie die Helligkeit
der Sonne von der Position auf der Sonnenscheibe abhängt. Aber weil der Sonnenrand einen scharfen
Sprung von hell nach dunkel darstellt, können wir aus der Gestalt des Sonnenrandes auf die Breite
der Antennenkeule schliessen.
Breite Keulen
|
Wollen wir einen kompletten Driftscan erhalten, braucht es eine genaue Positionierung der Antenne.
Wir fahren die Antenne auf eine Position, bei der die Sonne einige Zeit später sein wird. Da sich der
Himmel in 4 Minuten um 1° bewegt, brauchen wir bei einer HPBW von 3° eine Position 9°
oder 36 Minuten später. Mit der Antenne an dieser Stelle, beginnen wir nun die ständige Aufzeichnung
der Signalstärke. Nach dem Durchgang durch ein Maximum warten wir solange, bis das Signal wieder auf einen
kleineren und konstanten Wert heruntergekommen ist ...
dies sollte das Rauschen des leeren Himmels sein. Unter Umständen steigt das Signal wieder etwas an, weil
wir in eine Nebenkeule geraten ... Daher sollte es eine gute Idee sein, die Antenne bei gleicher Elevation
ein gutes Stück nach links (Osten) zu drehen, und dort die Stärke des Himmelsrauschen nochmals zu messen.
Denn dieser Wert ist wichtig!
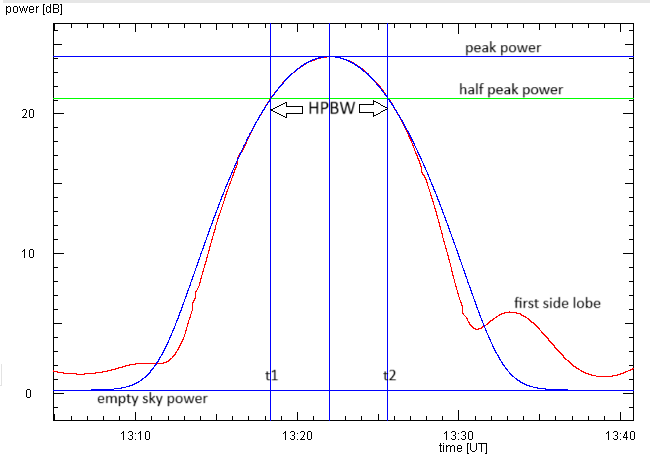
Interpretation: Sind die aufgezeichneten Leistungswerte in dB, müssen wir sie erst in lineare Leistungen
umwandeln (p = 10dB/10). Die gemessene Leistung ist die Summe aus dem Sonnenrauschen und dem
Rauschen der Erdatmosphäre, durch die die Radiowellen von der Sonne zu uns gelangen. Der Mittelwert für das
Rauschen des leeren Himmels ist also die Leistung ohne die Sonne. Diesen Mittelwert ziehen wir von allen
Driftscanwerten ab, um die Leistung der Sonne zu erhalten und zu plotten. In den beiden Seiten der
glockenförmigen Kurve suchen wir die Zeitpunkte, an denen das Signal die Hälfte des Maximumsignals ist.
Dann rechnen wir die Zeitdifferenz in einen Winkel um:
HPBW = (t2-t1) * 0.25°/min * cos(decsun)
wobei decsun die Deklination der Sonne ist (viz. der Abstand vom Himmelsäquator). Der
Grund für diese Korrektur mit dem Deklinationswinkel ist, dass ein Objekt am Himmelsäquator mit
0.25°/min über den Himmel zieht, aber ein Objekt an den Polen fest zu stehen scheint, weil es auf der
Rotationsachse der Erde liegt.
|
Ein andere Möglichkeit ist der halbe Driftscan:
|
Dieses Verfahren benötigt nur die halbe Zeit. Ausserdem funktioniert es auch dann, wenn die Positionierung
der Antenne ungenau oder nicht stabil genug ist, um die Antenne genau auf die erforderliche Position zu
bringen. Wir richten die Antenne einfach auf die Sonne, bis das Signal am stärksten ist. Dann stellen
wir die Antenne fest, und beginnen mit der Aufzeichnung der Signalstärke. Wir warten bis das Signal
auf einen niedrigen konstanten Wert abgefallen ist. Am besten ist es, dann die Antenne noch ein gutes
Stück nach links (Osten) zu drehen, um dort das Rauschen des leeren Himmels zu messen, denn dies ist
die Leistung ohne die Sonne.
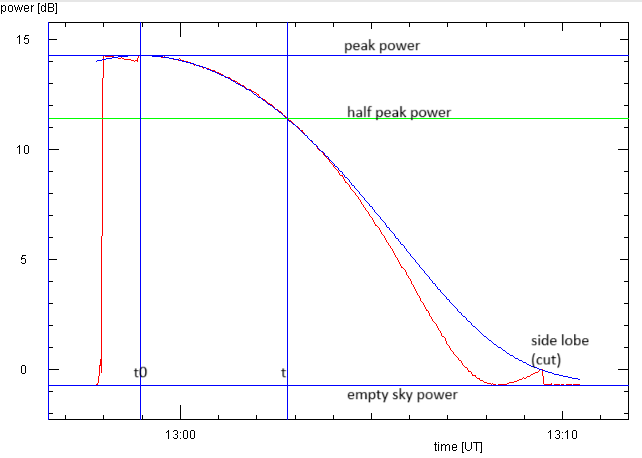
Interpretation: Sind die aufgezeichneten Leistungswerte in dB, müssen wir sie erst in lineare Leistungen
umwandeln (p = 10dB/10). Die gemessene Leistung ist die Summe aus dem Sonnenrauschen
und dem Rauschen der Erdatmosphäre, durch die die Radiowellen von der Sonne zu uns gelangen. Der Mittelwert
für das Rauschen des leeren Himmels bildet den Nullpunkt für die Sonnenleistung. Diesen Mittelwert ziehen
wir von allen Driftscanwerten ab, um die Leistung der Sonne zu erhalten
und zu plotten. In der abfallenden Seite suchen wir den Zeitpunkt, an dem das Signal auf die
die Hälfte des Maximumsignals gefallen ist. Dann rechnen wir die Zeitdifferenz in einen Winkel um:
HPBW = 2 * (t-t0) * 0.25°/min * cos(decsun)
wobei decsun die Deklination der Sonne ist (viz. ihr Winkelabstand vom Himmelsäquator).
Der Grund für diese Korrektur mit dem Deklinationswinkel ist, dass ein Objekt am Himmelsäquator mit
0.25°/min über den Himmel zieht, aber ein Objekt an den Polen fest zu stehen scheint, weil es auf der
Rotationsachse der Erde liegt.
|
Schmale Keulen
|
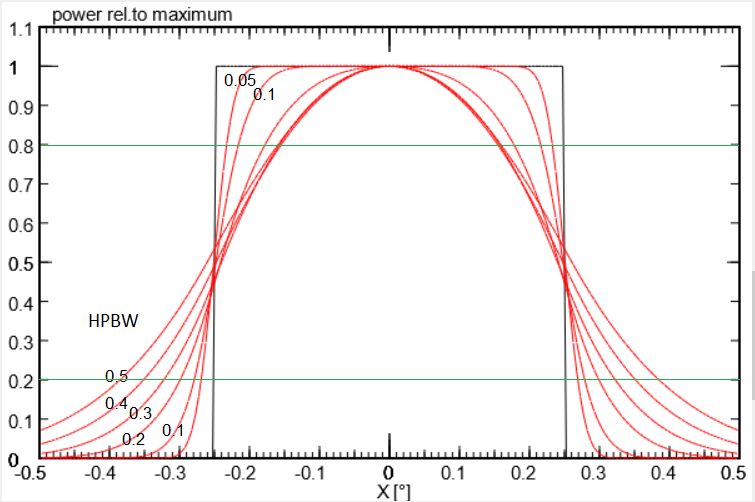
Die Sonne kann recht gut als eine gleichmässig helle Scheibe angesehen werden (schwarze rechteckige Kurve).
Wenn wir sie mit einer schmalen Antennenkeule betrachten (HPBW < 0.05°), bekommen wir ein Helligkeitsprofil
mit einer abgeflachten Spitze. Verwenden wir aber eine Keule, die viel breiter als 0.5° ist,
ergibt der Driftscan eine glockenförmige Kurve, dessen Gestalt die Empfindlichkeitskurve der Hauptkeule ist,
und deren Breite direkt die Halbwertsbreite HPBW ist - dies ist der Trick, der uns erlaubt, mit der Sonne
die Breite von breiten Antennenkeulen zu messen, wie oben beschrieben.
Ist nun aber die HPBW mit dem Sonnendurchmesser vergleichbar, so wird die Driftscankurve ein Mittelding zwischen
diesen beiden Extremfällen sein, und ihre Deutung wird etwas komplizierter sein. Glücklicherweise ist
die stärkste Änderung am Sonnenrand zu erkennen: der scharfe Sprung von grösster zu kleinster Intensität
wird durch die Antennenkeule in einen allmählich abklingenden Übergang ausgewaschen. Da eine breitere
Keule den Übergang flacher und breiter macht als eine schmalere Keule, können wir dies nutzen, um die
HPBW zu messen. Wir tun dies, indem wir die Zeit messen, die zwischen zwei Intensitätsschranken vergeht
- zum Beispiel bei 80% und 20% der Maximalintensität. Dann benutzen wir die Erdrotation, um die Breite
des Sonnenrands zu berechnen
RandBreite = (t20 -t80) * 0.25°/min * cos(decsun)
(hier für den rechten (ausgehenden) Rand). Die untere Tabelle erlaubt uns die HPBW zu bestimmen, die die
Randbreite bei den benutzten Schrankenwerten erklärt.
|
Die Randbreiten [in °] einer gleichmässig hellen Kreisscheibe mit Winkeldurchmesser 0.5° mit scharfem Rand, wie sie
von einer Antennenkeule mit HPBW zwischen 0.05 und 0.5° als Winkel zwischen den beiden Punkten gemessen wird, an denen
die Intensität auf 15%/85% ... 30%/70% der maximalen Intensität abgefallen ist.
| HPBW[°] levels = | 0.15/0.85 | 0.2/0.8 | 0.25/0.75 | 0.3/0.7 |
| 0.05 | 0.043 | 0.035 | 0.028 | 0.022 |
| 0.1 | 0.088 | 0.072 | 0.057 | 0.044 |
| 0.2 | 0.179 | 0.146 | 0.117 | 0.091 |
| 0.3 | 0.244 | 0.200 | 0.161 | 0.126 |
| 0.4 | 0.293 | 0.240 | 0.193 | 0.151 |
| 0.5 | 0.341 | 0.279 | 0.225 | 0.176 |
| 1.0 | 0.610 | 0.500 | 0.402 | 0.313 |
Diese Tabelle wurde mit einer Version des Javascript Programms
LunarDriftScans berechnet, die auf
dem Internet zur Verfügung steht. Dieses Werkzeug sagt das Radiobild des Mondes bei jeder Frequenz und Mondphase voraus,
und zeigt die zu erwartende Kurve eines Driftscans. Es errechnet daraus die Breiten des Mondrandes, bei vorgegebenen
Intensitätsschranken. Es kann daher unsere Daten auswerten, insbesondere des Mondes dessen Radiobild sich mit der Mondphase
ändert.
Beachte:Bei der Auswertung von Sonnen-Driftscans, wählt man einfach eine niedrige Frequenz (1 GHz),
um die Mondscheibe genauso gleichmässig hell wie die Sonnenscheibe zu machen.
Siehe DUBUS 2/2023, 6.
|
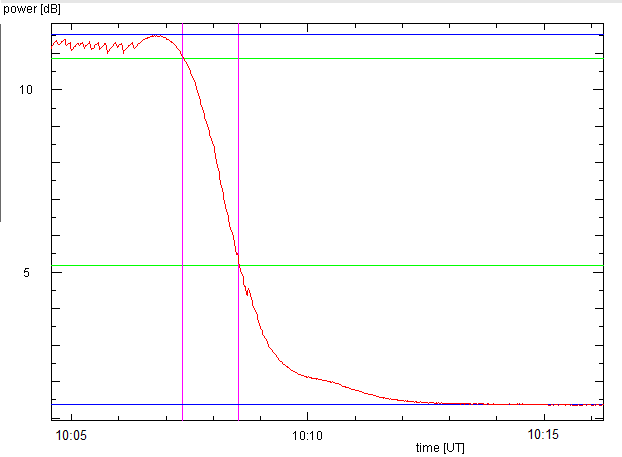
Hier ist ein halber Driftscan der Sonne, aufgenommen mit dem 3.7 m Spiegel auf 24 GHz im Jahre 2014.
Wir suchen zunächst das stärkste Signal von der Sonne, setzen dann die Antenne ein klein wenig nach Westen,
und schalten die automatische Nachführung aus, und lassen die Sonne durch die Antennenkeule wandern.
Die blauen Linien markieren die Intensitäten von Sonne
und leerem Himmel (die das Nullniveau der Sonnenhelligkeit darstellt). Die grünen Linien zeigen
die Intensitätsschranken von 15% und 85% an. Die Randbreite von 0.28° gibt eine HPBW von 0.38°.
Mit dem AntennaCalc tool
finden wir, dass ein gleichmässig ausgeleuchteter Spiegel vom 3.7 m Durchmesser eine HPBW von 0.2° hätte.
Dies bedeutet, dass die Antenne eine Apertureffizienz von nur 28% besitzt, oder dass der Spiegel nur in
einen Effektivdurchmesser von 2 m ausgeleuchtet ist. Messungen mit dem Mond bestätigten diese sehr enttäuschenden
Werte.
|
|
Es gibt eine lange Geschichte mit dem 3.7 m Spiegel auf 24 GHz. 2014 ergab die Messung der HPBW 0.38°,
was einen Apertur-Wirkungsgrad von bloss 28% bedeutet, und darauf hinwies, dass der Spiegel nur bis 2 m
Durchmesser ausgeleuchtet wird. Auch war die Sonne etwa 10 dB über dem Himmelsrauschen, und der Mond 0.7 dB.
Offensichtlich konnte man damit nicht zufrieden sein ... Schliesslich wurde ein neues Feedhorn installiert
und weitere Verbesserungen ausgeführt ...
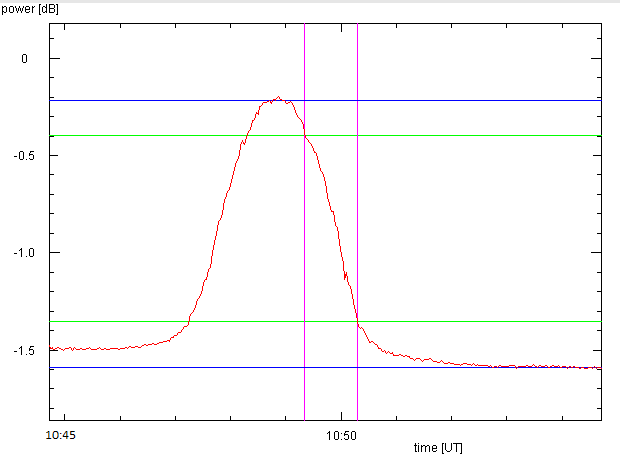
Die neuen Messungen von 2021 - es genügt nur den Mond zu zeigen - erbrachten wesentliche Verbesserungen:
Die Sonne ist 13.5 dB über dem Himmel, der Mond 1.4 dB. Sowohl Sonne als auch Mond geben Randbreiten
von 0.22°, was eine HPBW von 0.26° bedeutet. Der Wirkungsgard beträgt 60% und der Effektivdurchmesser
2.9 m. Der Gewinn ist 57.2 dBi, eine grosse Verbesserung gegenüber 53.8 dBi von 2014.
Leider gibt es wegen eines temperaturempfindlichen Verstärkers für das lange Kabel in der Zwischenfrequenzkette
eine ärgerliche Drift in der Verstärkung. Daher werten wir hier nur einen Rand aus.
|





